通过详细的示例和应用掌握集成的艺术
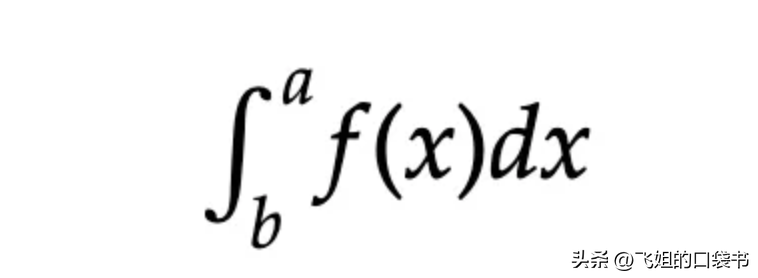
微积分和积分简史
曾几何时,在数学的神秘国度,艾萨克·牛顿爵士和戈特弗里德·威廉·莱布尼茨爵士这两位才华横溢的头脑独立地发展了微积分的基础。这个关于竞争和智力实力的史诗故事始于 17 世纪后期,当时两位数学家都试图解开不断变化的数量之谜。

关于究竟是谁发明了微积分一直存在很多争议,大多数人主要归功于牛顿。真相有点模糊。尽管牛顿和莱布尼茨都对微积分的发展做出了贡献,但正是莱布尼茨引入了我们今天使用的积分符号。这个漂亮的小符号 (∫) 代表一个拉长的“S”,代表“summa”(拉丁语的“sum”),这是有道理的,因为积分本质上是将无限小的部分相加以找到一个整体的艺术。
积分在各个领域的重要性
积分听起来像是一种神秘的数学咒语,但它们在许多领域都发挥着关键作用。从计算曲线下的面积到确定力所做的功,积分是数学世界的主力,当我们需要找到累加量时,它会承担繁重的工作。
一些关键依赖积分的领域包括物理学(想想流体动力学和电磁学)、工程学(用于结构分析和控制系统)、经济学(计算边际成本和消费者剩余),甚至医学(用于模拟生物过程)。
简而言之,您根本无法摆脱任何类型科学中的积分!

现在我已经满足了您的好奇心,是时候揭示我对这个集成系列的总体规划了。我会:
- 介绍积分的基本概念,包括它们的定义、规则和性质。
- 揭示以风格和技巧解决积分的秘密技巧。
- 深入研究整体应用领域,探索它们在现实世界中的无数用途。
- 提供令人愉悦的示例自助餐,从简单到让人胃口大开到极其复杂。
- 提供提示和技巧,帮助您成为集成向导,甚至能够应对最艰巨的微积分挑战。
所以,亲爱的读者,拿起你的数学帽子,加入我的积分之旅吧!
整合的定义

整合,本质上是分化的逆过程。微分可以帮助我们找到函数的变化率,而积分则可以找到累积的变化或原始函数本身。把它想象成拼图,每个无穷小的部分都有助于构成整体的宏伟杰作。
从数学上讲,积分可以表示为:
∫f(x) dx
其中 f(x) 是被积分的函数,dx 表示我们求和的每一部分的无限小宽度。积分符号(∫)提示我们深入积分过程。
积分的正式定义是基于黎曼和的概念。黎曼和是定积分的近似值,通过将曲线下的面积划分为有限数量的矩形并将它们的面积相加。我们使用的矩形越多,我们的近似值就越准确。
让我们考虑区间 [a, b] 上的连续函数 f(x)。要计算此区间上 f(x) 的定积分,我们遵循以下步骤:

当我们这样做时,我们看到黎曼和因此等于:
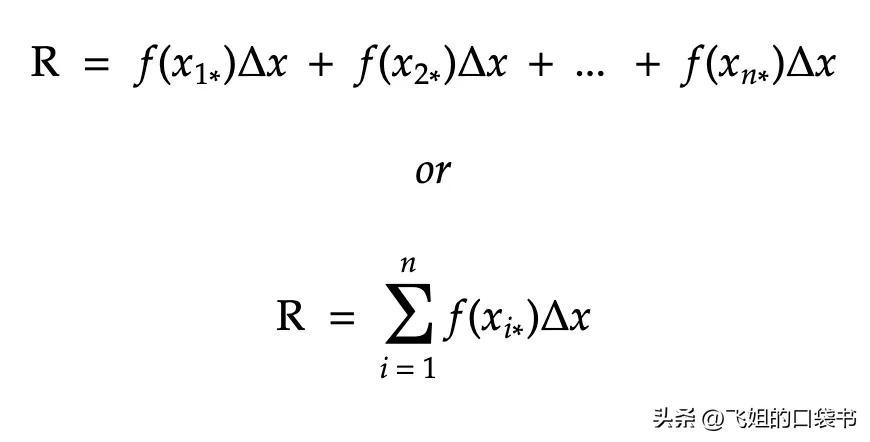
现在,为了正式定义定积分,我们将极限视为子区间数 (n) 接近无穷大:
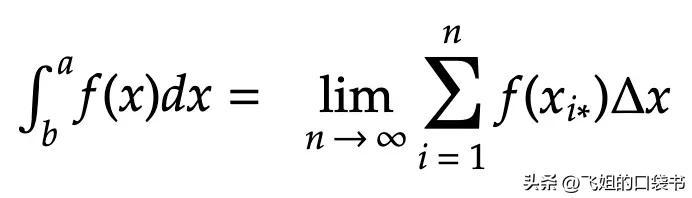
需要明确的是:对于每个子区间 i,我们选择一个唯一的样本点 x_i* 来评估函数 f(x) 并将结果乘以子区间的宽度 Δx。然后,我们将所有 n 个子区间的结果乘积求和以形成黎曼和。最后取n趋于无穷大的极限求定积分,表示函数f(x)在区间[a,b]内曲线下的确切面积!
使用黎曼和的积分的正式定义有助于我们理解将无限小的部分相加以找到整体的基本概念。然而在实践中,我们通常应用各种积分技术和规则直接计算定积分,因为这些方法更有效和方便。
不定积分和定积分
积分有两种形式:不定积分和定积分。
不定积分:不定积分,也称为反导数,代表一族函数,其导数是原始函数 f(x)。不定积分没有极限,表示为:

其中 F(x) 是反导数,C 是积分常数。这个常数的产生是因为当我们微分一个常数时,我们得到零;因此,可能存在仅相差一个常数值的多个反导数。
定积分:另一方面,定积分计算函数在指定区间 [a, b] 内的累积变化。它表示为:
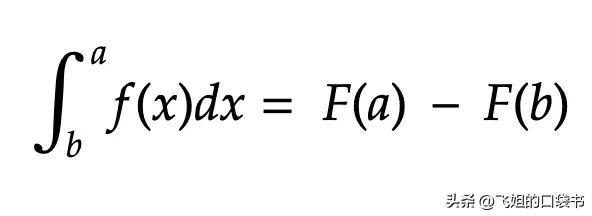
其中 F(x) 是反导数,a 和 b 是积分极限。与不定积分不同,定积分给了我们一个特定的数值。